• Run model
• Quick start
• Introduction
• Model details
  
• FAQ
• Basic Model
• About GunderFish
• Contact Us

Advanced GunderFish CoVID-19 Model

This model is for educational purposes only. If you would like more information, contact us.

GunderFish Outbreak Model

Design Details and Algorithm Specification

1 Introduction

The effects of a disease outbreak are often devastating to the region affected and often seem inexplicable to the general population. The GunderFish Outbreak Model is an attempt to give a basic understanding of the disease spread process to a non-technically trained person. This paper is aimed at the technically trained individual who wants a better understanding of the internal workings of the simulator.

The paper is organized as follows:

• An overview of the components in the disease spread and the underlying data structures used to represent the model,
• Details about the spread propagation algorithm and assumptions,
• The steps taken to ‘tune’ the model and the sources for the underlying constants, and
• Some examples of the results along with a look at the next steps.

2 Mathematical Model Description

The XSD (eXplore Social Distancing) simulator model is designed as a tool to explore the effects of social distancing and quarantine controls applied to a disease outbreak.

It builds a population and tracks the transitions of groups of people (cohorts) as they are exposed, become infected, show symptoms and spread the disease, until they have a resolution – either recovering or (in the case of a potentially fatal disease) they die from the infection.

The model provides the ability to describe the characteristics of an infectious disease and to describe the ‘cultural’ components of a population. These cultural components include things like how gregarious they are (how many people do they have close contact with on a daily basis), how responsible they are (do they tend to stay home if they are sick, or do they keep going to work), and other social aspects that mark the difference, say, between a New York office worker and a rural Colorado accountant.

2.1 Overview

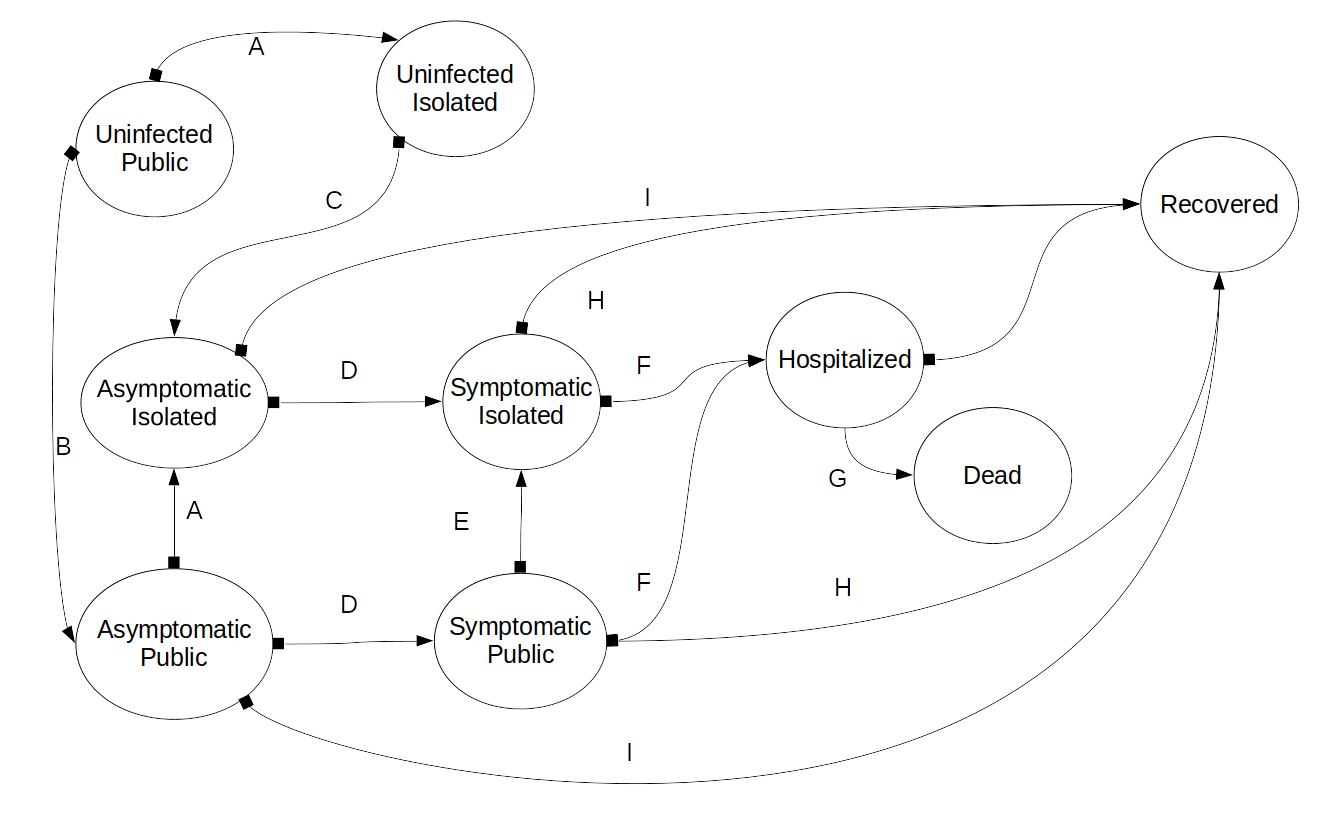
We are representing the affected population of a location with a Transition Graph model. This model consists of nodes and edges. The nodes represent a specific state, and the data of how many individuals are in the state at the current period. The edges represent the allowed transitions from one node to another.

2.1.1 Model States

The states are:

• Uninfected Public – this is where everyone starts, no infection, going about your daily business
• Asymptomatic Infected Public – these are people who have been infected and don’t know it yet
• Symptomatic Infected Public – these are people who know that are infected, but still go about their daily routine
• Uninfected Isolated – these are people who have chosen to isolate themselves, even though they are not infected
• Asymptomatic Infected Isolated – these are people who have chosen to isolate themselves, even though they don’t know that they are infected
• Symptomatic Isolated – these are people who have chosen to isolate themselves, because they are infected
• Hospitalized – these are people who have gotten sick enough to go to the hospital
• Recovered – these lucky people have recovered and are immune
• Dead – this is obvious

2.1.2 Model transitions

The model has a set of transitions representing the progression of the disease and the response of individuals to the disease. In Illustration 1, these are shown as the arrows labeled A-K. The semantics of the transitions are:

1. People who are not infected (or are asymptomatic) who choose to self-isolate.
2. Uninfected people in public who become infected.
3. Uninfected people in isolation who become infected despite their isolation
4. Asymptomatic people who begin to show symptoms.
5. People in public who show symptoms and isolate themselves, or enter the hospital and become isolated
6. Symptomatic people in the general public who go to the hospital.
7. Symptomatic people in isolation who go to the hospital.
8. Hospitalized people who die (in this model only people who go to the hospital die, clearly hospitals cause death).
9. Hospitalized people who recover.
10. Symptomatic people who recover.
11. Asymptomatic people who recover.

The details of these transitions are covered in Section 2.3.

2.2 Creating a Transition Graph Model

The basic model tracks the transitions in the state of the people being modeled. The complete flow is shown in Illustration 1. It focuses on the progression of the disease through the population, by modeling the disease states (uninfected, asymptomatic, symptomatic, recovered, dead) and the accessibility (public, isolated) of the individual. The disease is modeled with descriptive parameters (transmission rate, time to symptoms, time to resolution, probability of symptoms, etc.). The social/cultural aspects ( average number of close contacts per period, likelihood of self isolation, etc.) of the subject population are also parameterized.

The model is a transition graph automaton, with a fixed transition period. The nodes (see Illustration 1) represent the number of people in each state in the current period. However, rather that representing these people as a single count (e.g., 45,000 people are infected) we must also keep track of when these people entered the state.

This need to track when the separate populations entered the state is why a simple Markov model cannot be used. The Markov model requires ‘path independence’ of the members in a given state. This model retains path information in the form of time of entry in order to properly progress from one period to the next.

Since the disease has a relatively fixed progression, for example 6 days from infection to showing symptoms, we need to know that of the 45,000 people in the example above, 2000 were infected 5 days ago, 6000 were infected 4 days ago, etc. Only the group that was infected 5 days ago will be suitable for transition to ‘symptomatic’ during this period. We represent these sub-populations as cohorts of the number of individuals and the times at which significant transitions occur.

Each period, each of the cohorts, in each of the nodes (the state) is analyzed, and portions are transitioned into the appropriate state for the next period. For example, the uninfected public count is assessed by the various disease-specific and cultural-specific parameters and the model determines how many of the uninfected become infected. These are added to the asymptomatic public node as a new cohort, with the appropriate ‘time of infection’ included. This newly infected cohort is removed from the uninfected public node and added to the asymptomatic public node. They are added to the asymptomatic public node because they have not yet begun to show symptoms. The portion of the original uninfected public cohort that did not get infected is represented by reducing the uninfected cohort count.

Illustration 1: Basic Transition Graph Automata Flow model for a disease outbreak.

2.2.1 Flow ordering assumptions

The basic flow ordering is:

1. process respose to social controls
2. process disease resolution (death, recovery)
3. process asymptomatic to symptomatic transitions
4. process symptomatic to hospitalization transitions
5. process public to isolated transitions (only for people who become symptomatic)
6. process new infections

The specific parameter definitions and transition equations are described in the next section, and the algorithm is presented in more detail in Section 2.4

2.2.2 Variables

• Social controls
  • I_a= Self isolation rate of uninfected and asymptomatic people
  • I_s= Infected self isolation rate after becoming symptomatic (after t_o days)
  • N_p= Number of contacts per time period of a public individual
  • N_i= Number of contacts per time period of an isolated individual
• Disease constants
  • t_n = Day of infection
  • t_s = Number of days from infection to symptoms
  • t_h = Number of days to hospitalization, from the onset of symptoms
  • t_r = Number of days to resolution (recovery or death) for the hospitalized from the onset of symptoms
  • t_c = Number of days to recovery for asymptomatic and symptomatic (not hospitalized) from the date of infection
  • A = the probability of an infected person becoming symptomatic
  • T = the transmission rate, likelihood of infection during contact between an infected and an uninfected person
    • note that
      • R_0p =T * R_p * t_c and
      • R_0i =T * R_i * t_c
  • F = Fatality rate for hospitalized patients
  • H = Hospitalization rate for symptomatic patients
• Counts, Probabilities, and Rates
  • C_up(t) = Count of uninfected public at time t
  • C_ap(t) = Count of asymptomatic public at time t
  • C_sp(t) = Count of symptomatic public at time t
  • C_ui(t) = Count of uninfected isolated at time t
  • C_ai(t) = Count of asymptomatic isolated at time t
  • C_si(t) = Count of symptomatic isolated at time t
  • C_u(t) = Count of all uninfected at time t
  • C_a(t) = Count of all asymptomatic at time t
  • C_s(t) = Count of all symptomatic at time t
  • C_h(t) = Count of hospitalized at time t
  • C_r(t) = Count of recovered at time t
  • C_d(t) = Count of dead at time t

2.3 Transitions

1. This is the rate at which uninfected and asymptomatic people choose to isolate themselves. This will happen either at the start of the model, on the arrival of new people to the model, or in the period when rates are changed.
   For the uninfected C_u*I_a people will be moved into uninfected isolation
   For the asymptomatic C_a*I_a people will be moved into asymptomatic isolation
   The remaining will stay in the public state.
2. This is number of uninfected people in public who catch the disease. They become asymptomatic. If they started in a public state they will remain in a public state and if they started in an isolated state they will remain in an isolated state. This occurs in every time period.
   This rate is a function of the number of contacts that an uninfected person has and the infection status of the people contacted.
   The total number of contacts available n_x = N_p*(C_up+C_ap+C_sp) + N_i*(C_ui+C_ai+C_si)
   The total number of infected contacts available n_n = N_p*(C_ap+C_sp) + N_i*(C_ai+C_si)
   Therefore the probability of a contact being infectious is P_n = n_i/n_x
   For a group, the number of infections will be a function of the number of contacts each member of the group has, the probability of infectious contact, the transmissivity of the disease, and the number of individuals in the group
   For the uninfected public C_ap(t) = P_n*T*N_p*C_up(t-1) + C_ap(t-1)
   For the uninfected isolated C_ai(t) = P_n*T*N_i*C_ui(t-1) = C_ai(t-1)
3. This is the number of uninfected isolated people who become infected, in spite of their best efforts, and stay in isolation. The derivation is the same as for transition B.
   For the uninfected isolated C_ai(t) = P_n*T*N_i*C_ui(t-1) + C_ai(t-1)
4. This is the number of infected people who become symptomatic (at this point they are still in the general population). This occurs to people who were infected t_s time periods ago. This applies regardless of whether they are isolated or in public.
   C_sp(t)= C_ap(t_n + t_s)*A + C_sp(t-1)
   C_si(t)= C_ai(t_n + t_s)*A + C_si(t-1)
5. This is the number of symptomatic infected people who go into isolation. They will either self-isolate on the day of arrival or on the day when they first show symptoms.
   C_ai(t) = C_ap*I_s(t-1) + C_ai(t-1)
6. This is the number of symptomatic infected people in the general population who go to the hospital. This occurs to people who became symptomatic t_h periods ago.
   C_h(t) = C_sp(t_s + t_h)*H + C_h(t-1)
   C_h(t) = C_si(t_s + t_h)*H + C_h(t-1)
7. This is the number of symptomatic people in the hospital who die. The remainder recover. This occurs to people who became symptomatic t_h periods ago.
   C_d(t) = C_h(t_s+t_r)*F + C_d(t-1)
   C_r(t) = C_h(t_s+t_r)*(1-F) + C_r(t-1)
8. At the end of t_c all of the asymptomatic people recover.
   C_r(t) = C_ai(t_s+t_c) + C_ap(t_s+t_c) + C_r(t-1)
9. At the end of t_c all of the symptomatic people recover.
   C_r(t) = C_si(t_s+t_c) + C_sp(t_s+t_c) + C_r(t-1)

2.4 Algorithm

These are the algorithms that enable the model to predict the state of the entire population at the next time step. Note that may of these are dependent on the results of a previous calculation, so they must be done in order.

1. If there has been a change in isolation rates (symptomatic or asymptomatic)
   1. Move people between isolated and public states
2. Resolve hospitalized cases
   1. Transfer the number of new fatalities from hospitalized to dead
   2. Transfer the number of recovered from hospitalized to recovered
3. Calculate the new recovered
   1. Transfer the number of new recovered from the symptomatic infected (public and isolated) to recovered
   2. Transfer the number of new recovered from the asymptomatic infected (public and isolated) to recovered
4. Infection rates
   1. Transfer uninfected public to asymptomatic infected public
   2. Transfer uninfected isolated to infected isolated
5. Transfer to Isolation
   1. Transfer newly symptomatic public to symptomatic isolation according to existing social controls

This algorithm was coded in Java, with a PHP and Javascript front end.

3 Tuning

3.1 Estimating parameters

Transmission rate: In this model we use an R per day rather than the more traditional R₀, where

• R_t= Transmission rate(T) * number of contacts per day

An estimate of the R_t can be found by analyzing the first deaths in the outbreak. The infections that caused these deaths will have occurred before the public became alarmed and should therefore represent the R_t of that population in its normal state. The model approximated the death rate in Denver if the R_t was set at 0.224. We researched the contact rate of a medium sized city, and estimated Denver's contact rate at 32 people/day. We also assumed a small pre-infection self isolation rate (95%) (Mostly people who were watching the news from China). This resulted in a transmission rate of 0.007 infections per contact. Note that, assuming a transmission time in the population of 10 days, this results in a R₀  of 1.85.

Initial Cohort size: We estimated the inital population by comparing the death rate in the model to the actual death rates in Colorado. In order to validate the Covid death rates, we extracted excess death numbers from the CDC data on deaths. For the first 6 weeks of the epidemic, the excess death rates matched the reported Covid-19 death rates with an R² of 0.90. Using the Imperioal College death rate of 1% of death from infection, we estimated that approximately 1000 people were infected in Colorado on March 1. The Imperial college paper showed an asymptomatic rate of 50%, so we split the initial cohort into equal symptomatic and asymptomatic cohorts.

Hospitalization rate: Using these numbers we ran the model and compared the predicted hospitalizations to the actual hospitalization rates in Colorado. We discovered an infection to hospitalization rate of 4.2% in Colorado. Note that this is half as much as the 8.8% reported by the Imperial College paper in Wuhan. This may be a result of differing health care systems.

Hospitalization to death rate: By experimentation with the model, we derive a hospitalization to death ration of 31%. In the early stages of the infection, this number was significantly higher, but it stablized to this value after approximately 60 days

3.2 Timing

The initial timing values are taken from the Imperial College paper. Once the state began to apply social controls, we were able to estimate the timing of of hospitalization and death for Colorado more accurately.

• t_o = Number of days to symptoms = 5 days.
• t_o = Asymptomatic to recovery = 7 days.
• t_o = Number of days from mild symptoms to recovery = 7 days.
• t_o = Number of days from symptoms to hospitalization = 6 days. This was changed from 5 days to 6 day after experimentation with the model.
• t_r = Number of days to resolution from hospitalization (recovery or death) = 17. This was changed from approximately 12 days to 17 days after experimentation with the model. This may be due to the difference in hospitalization rates, observed above. The ratio of serious cases to less serious cases using the hospital system may be different.

3.3 Inital Setting

• The number of contacts/day that an unisolated person will have. Note that the number of contacts that an isolated person will have is set to 5.
• The initial population of the area
• The number of available hospital beds. Note that this is just used for display purposes, and does not change the death rate when the hospitalization exceeds the available hospital beds.
• The deaths on the 28th day, this is used to load the model with infections at the rate of 65 deaths/10000 infections, with 50% of the infections being asymptomatic.

3.3 Social controls

In this model there are four social controls

• I_a = Self isolation rate of asymptomatic people. This is initially set to 0.0.
• I_s = Infected self isolation rate after becoming symptomatic (after t_o days)This is set to
• N_p = Number of contacts per time period of a inisolated individual. We assume that the contacts of an infected individual will stay at 5
• Percentage of masking. The research varies greatly in the estimate of the impact of masking on transmittion, from 30% (Mitze et al, 2020) to 70% (Kai et al). We assume that for an unisolated individual masking will reduce contact by 50%

4 Examples

The simulator allows the operator to set up a sequence of responses to be enacted at specific times. It then produces a graph of the expected hospitalizations that would result. After connecting to the simulator, the operator sets up their response plan using the sliders in the setup table. Once the simulation is correctly configured, the operator simply presses the ‘run simulation’ button. The simulation executes and the resulting graph showing day by day hospitalization needs is presented.

4.1 No response

The simplest thing to do is nothing. In this case, the Governor of the state decides that no response policy is the correct response. The results are shown in Illustration 2, indicating that nearly 25,000 people required hospitalization on day 44. The horizontal blue line indicates the available hospital capacity of only 10,000 beds. This is not good – it indicates a lot of people dying due to the lack of hospital care.

Illustration 2: Effect of No Response to the Outbreak, approximately 25,000 people need hospitalization, overwhelming the healthcare system.

4.2 Stay at Home with Release

In this example, the governor responds to the outbreak after about 2 weeks of discussions and planning. She imposes a 45 day full “Stay at Home” order, which is released on day 60. This results in a lower peak hospitalization maximum (about 21,000) and it gives the state an extra 45 days to prepare. This time can be used to prepare additional hospital beds, or take other actions.

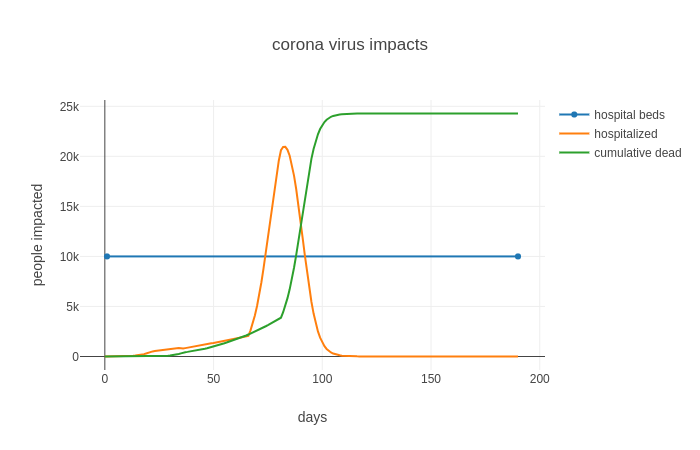
Illustration 3: In this simulation, the state is ordered on "Stay-at-Home" for 45 days, then released. The Peak is now at day 83, and is just over 20,000

5 Next Steps

At this point the model is using deterministic transitions, using mean values for the parameters, these will be expanded to use distribution values to facilitate the use of Monte-Carlo modeling.

The current model stops at the transition to symptomatic states, the model will be expanded to track transitions to include hospitalized, critical, and ICU states.

The current model does not include age distributions.

Additional work needs to be done on the social distancing in different cultures and under different condition.

We are in the process of ground-truthing the model. One of the challenges of training a model while the data are still being collected is that the data are often incomplete and are frequently inaccurate. A second challenge is that in the early stages of an outbreak, the availability of data is problematic. As more data become available, and as older data are corrected the model must often be ‘re-calibrated’ to correct for errors. This is an on-going problem with the COVID-19 outbreak.

6 References

Ferguson, Neil M., et al (2020, March 16). Impact of non-pharmaceutical interventions (NPIs) to reduce COVID-19 mortality and healthcare demand. Imperial College COVID-19 Response Team. https://www.imperial.ac.uk/media/imperial-college/medicine/sph/ide/gida-fellowships/Imperial-College-COVID19-NPI-modelling-16-03-2020.pdf

Mitse, Timo, et al (2020, June). Face Masks Considerably Reduce COVID-19 Cases in Germany:A Synthetic Control Method Approach. IZA – Institute of Labor Economics. http://ftp.iza.org/dp13319.pdf

Kai, De, et al (2020, April). Universal Masking is Urgent in the COVID-19 Pandemic:SEIR and Agent Based Models, Empirical Validation,Policy Recommendations. preprint. https://arxiv.org/pdf/2004.13553.pdf

If you want to discuss the details with us, use this link to send a message directly to the team at GunderFish. Contact GunderFish